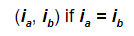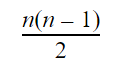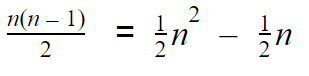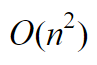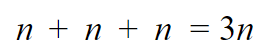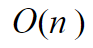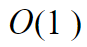|
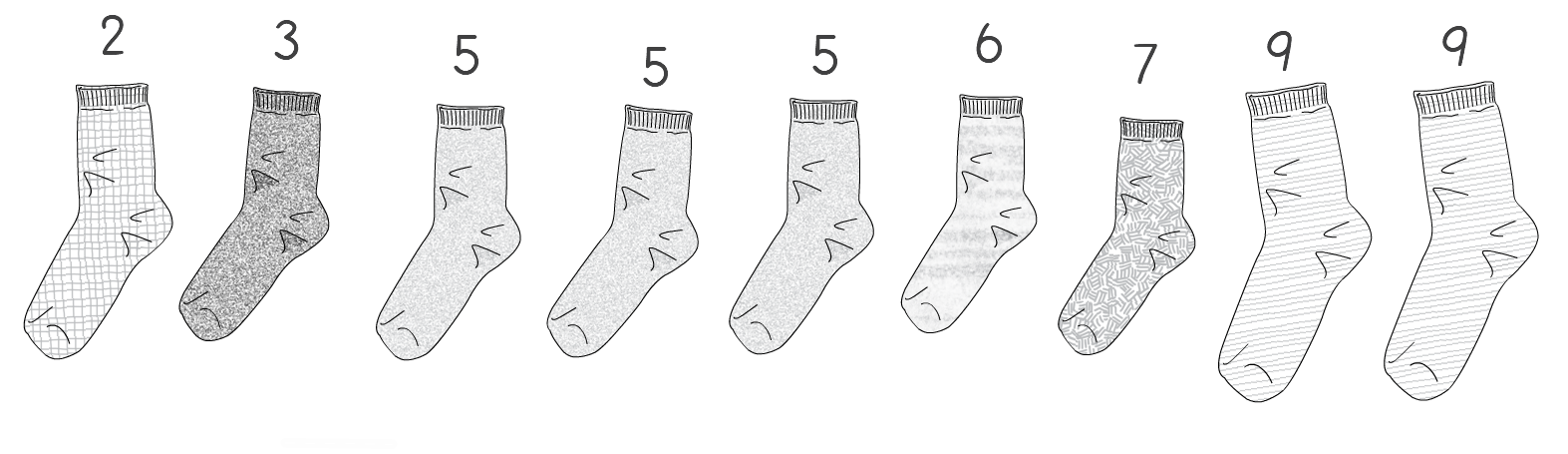
A few weeks ago I tweeted the following: “Looking for matching pairs of socks in the morning is always an O(n²) task for me. Anyone got a better algorithm?” I received a few responses which gave me the idea to use sock matching to explain big O notation. Right. Let’s start from defining the problem. Let’s assume we have n single socks and each matching pair is labeled with a number i. We define a pair of socks a and b as being a matching pair if Here’s a picture of an example of what I mean with the value if i on top of the sock: A couple of things to mention from the example picture above:
The aim here is to find any one matching pair. Think about when you wake up in the morning, open your sock drawer and need to find a pair that matches before going to work. If we had to write some code to represent this problem we could put the sock labels in a collection and feed it to a function that returns the label of any match found or a -1 if no match is found. A return of -1 means you’ll be going to work with flip flops. There are various approaches we can take in order to solve our problem. But how do we know which one is the best? And what does “best” even mean? If you’re like me and your mornings are always a bit of a logistical challenge, the “best” means the fastest way I can get out of the house. The problem is that speed is a slippery concept when it comes to algorithms. An algorithm might be fast in one type of input but perform poorly with another. So using speed alone is not a good indication. To go around this problem, in computer science, we don’t measure speed but scale. We ask the question: How bad will the program degrade as I increase the size of my input? The lower the degradation the better the algorithm will scale to larger inputs. To describe this, we use what is known as the Big O notation. The following sections try to give you an intuition of how we measure this by going through various examples. The Quadratic algorithmOur first attempt to solve this sock matching problem would be the way most of us do it when we’re in a hurry (although it’s also the slowest!):
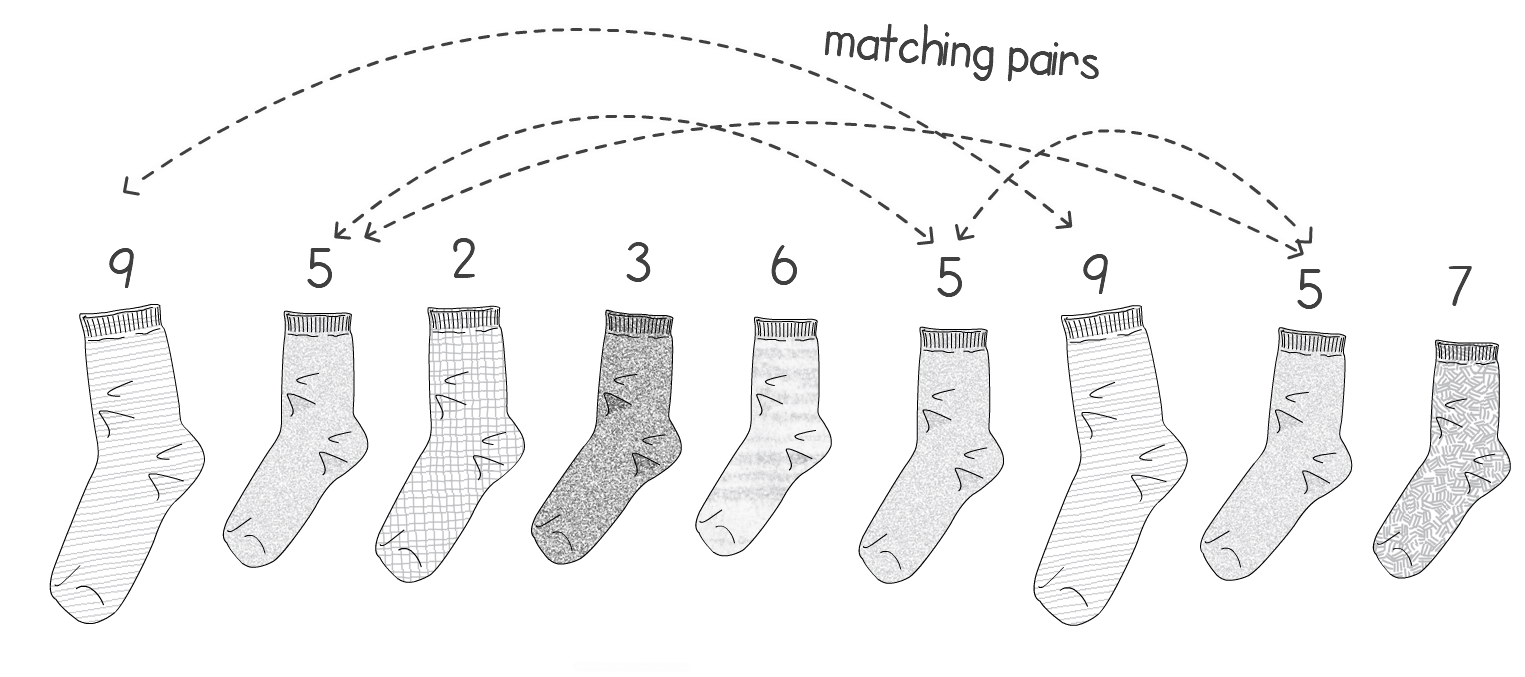
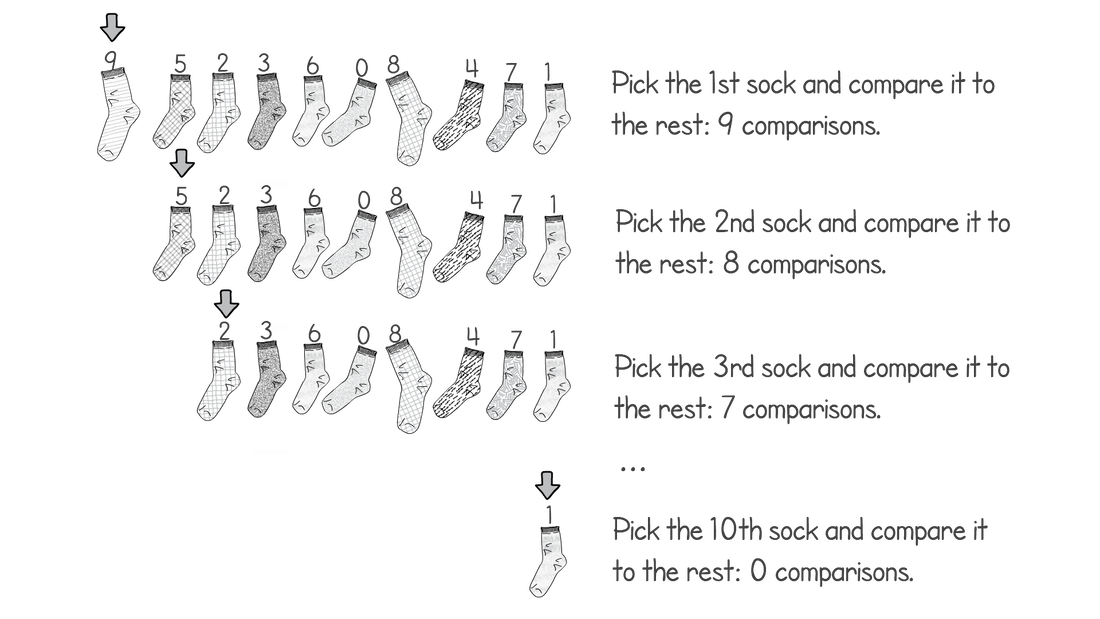
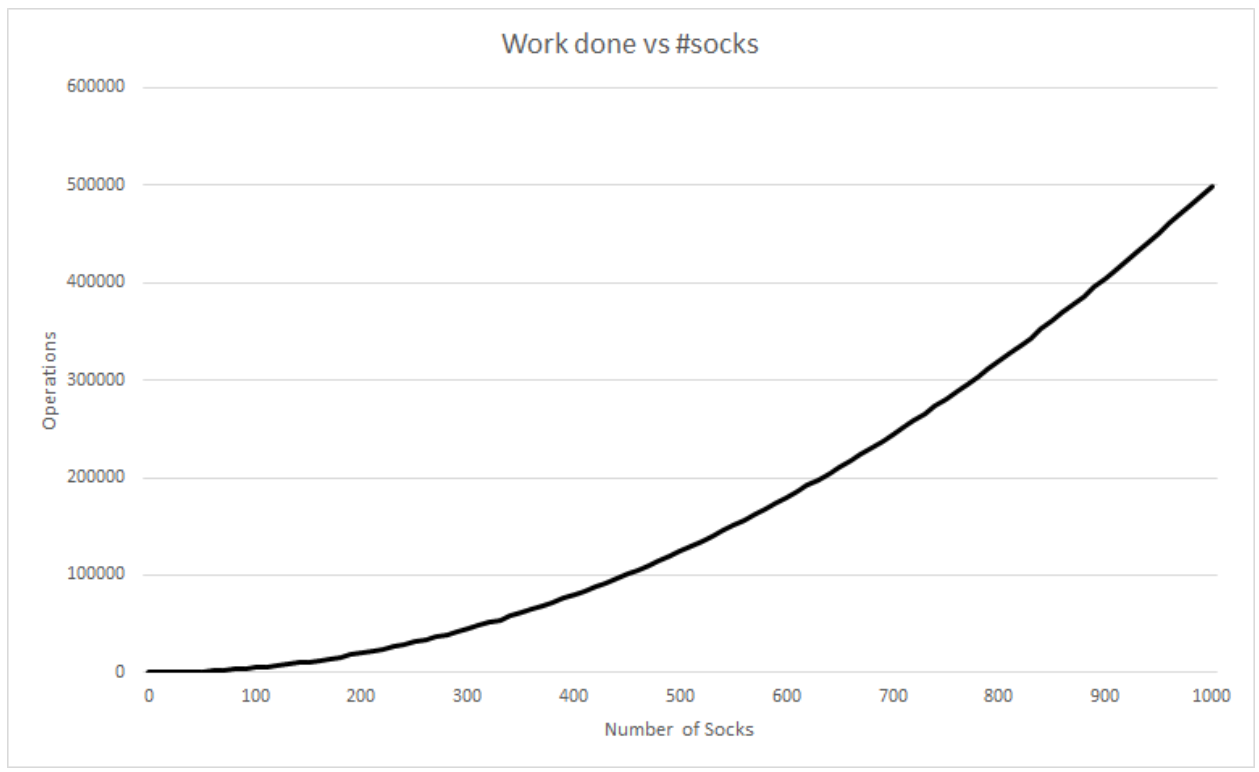
In python this can be written as: Say we have 10 socks in our pile. How many sock comparisons would we have to do with this setup? Of course that depends on the contents and way the pile is organized. If we’re lucky we’ll find two matching socks on the top of the pile, in which case we would only need to do one comparison (comparing the first two socks). This is called the best case scenario of an algorithm. Our best case does not change whether we had 10 or 1 million socks. If the first two socks match, we’ll always do one comparison. Although the probability of the best case occurring with 1 million socks is lower than 10 socks. The problem is that the best case doesn’t really tell us much about how good our technique is. We might be lucky a couple of times but it’s unlikely we’ll have the best case occurring every day in the long run, especially if we keep many socks. So we need another way to compare how good our solution is. Whenever we quote the Big O notation of an algorithm, typically we are referring to the worst case of the algorithm (although the average case is also used sometimes). The worst case is a much more useful measure to use to compare different approaches. If we know that an algorithm A is, in the worst case, better than algorithm B it will give us a better idea that A will perform better than B. This is the first rule when you come to compare algorithms using Big O notation. Use the worst case scenario. Sometimes you also want to compare the average case, but for the purpose of this article we’re sticking with the worst as it’s easier to understand and it’s usually enough. Right, can you think of the worst case scenario of our solution listed above? The worst case is when there isn’t a single matching pair in the pile. This is when you’re going to get to work late wearing mismatched socks. Now, for this worst case, try to work out the number of sock comparisons we need to perform if we had 10 socks at the start. So in total we would have done 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 + 0 comparison operations. If you sum this up it would give you 45. What if we had 100 socks instead of 10? This would result in 99 + 98 + 97… + 0 sock comparisons. There is an easy formula that would give us the result of this sum, without having to do the entire calculation: If we had to generalize for when we have an arbitrary number of socks n, we have: If you’re interested in how I got to the above expression, have a read through the wiki page: en.wikipedia.org/wiki/1_%2B_2_%2B_3_%2B_4_%2B_%E2%8B%AF#Partial_sums Fun fact: The above equation would also give you the total number of handshakes that would happen in a meeting with n people. What does this tell us about how good our algorithm is? Notice that when we increased the input (number of socks) by a factor of 10, from 10 to 100, our effort did not increase proportionally. For 10 socks we have to do 45 operations, however for 100 socks that number is 4950, not 450. How about we plot a chart with the input size vs the number of sock comparison operations we have to do? The above chart shows how much extra work we need to do as we increase our input. If it took us one second to compare a pair of socks, it would take us 1hr 20 mins in the worst case for 100 socks. If we increase the number by a factor of 10 again (1000 socks) it would take us almost 6 days to find a matching pair. So what is the Big O notation for our algorithm? We have already seen the expression that would give us the worst case scenario for this. We can expand that formula to give us: There are only two rules to convert any expression into Big O notation. First you drop any constants and then you only consider the part with the highest order. In our example the highest order of our expression is the squared part. Thus the above would result in: In geek speak we say that our sock matching algorithm has a quadratic worst case time runtime complexity or simply a Big O of n squared. The reason why we simplify the expressions in this way is that as n gets bigger and bigger, the parts of the expression with the lower orders count less and less. In practise, our algorithm is a little faster than n2 however this advantage gets less noticeable for large values of n. The Linear algorithmHow can we improve our sock matching? A friend of mine suggested keeping socks in some sort of order to make matching easier. This has never worked for me as the washing machine does a very good job of randomly shuffling them. For a moment let’s assume you do find a way to keep them sorted or maybe you order them as soon as they come out from the wash, how will our sock matching algorithm change? We can make use of the fact that the socks are sorted and we only need to match each sock to the one next to it. The algorithm would go something like this:
In python this can be written as: How does this affect our runtime performance? Again let’s think about our worst case performance, i.e. when we do most work. Again in this case this is when we cannot find a match and go through all of the socks. How many steps do we take? Let’s try to be more precise here. For almost each sock, we pick it up with the right hand, do a comparison and then pass it on to the left hand, i.e. 3 steps per sock. This means that if we had n socks the number of steps we take is: Now remember that to convert the above to Big O notation, we need to drop the constants and take the highest order. In this case we end up with: Notice that to derive the complexity of an algorithm we don’t have to be precise and count every single operation that the algorithm makes. If we only counted the sock comparisons instead of the picking up the socks in your hand, we would have arrived at the same expression. The important thing here is that we are consistent, we choose what to count and stick with it. This is what is called an algorithm with a linear runtime complexity and is usually what our mind defaults to when it thinks of proportions. Put simply, if you double the input size (number of socks) you also double the total number of operations. If it takes us 1 second to compare a pair of socks, it would take us 1000 seconds for 1000 socks, as opposed to the 6 days for the quadratic solution. Quite an improvement! Constant algorithmCan we improve even further? Another friend suggested that I throw away all my socks and buy many socks of the same type, colour and size. Genius and boring I thought… Our algorithm will now be very simple. Basically we just need to choose any two socks:
Any in python this would be: How does our performance change as we increase our input? First of all notice that in this case the worst case of the algorithm is the same as the best. Also it doesn’t matter if we have a couple of socks or a million. We will always perform the same couple of operations and the algorithm will take the exact same time. This is what we call a constant complexity, written as: A constant runtime complexity is the most scalable type and is usually the most desired type of algorithm. Notice that again it doesn’t matter how many operations we do in our algorithm as long as it doesn’t change when we change the input size.
It’s worth mentioning that computational complexity doesn’t tell us how fast an algorithm works for a particular input. It might well be that a constant algorithm might work slower than a quadratic one for a certain small input. If we only had two matching socks, all of our matching methods will perform quite well. Big O notation only compares how well different approaches scale with the input size. In our article we only explored three types of complexities, but there are many other types. Have a look at this wiki article to see all the different types of complexities: en.wikipedia.org/wiki/Time_complexity
1 Comment
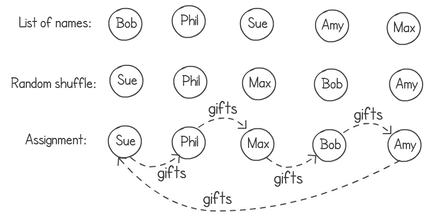
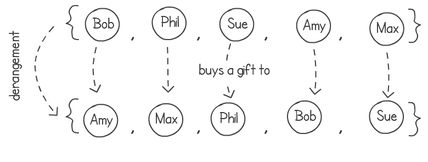
A few months ago I wrote about an algorithm to produce a random shuffle of an array. The idea was to use this algorithm for the Secret Santa game, where you have to buy a small gift for another team member. The following is a diagram illustrating how it would work in two steps. First we shuffle the list of names in an array, then we connect each name with the next, with the last name to the first. In this diagram Sue would buy a gift for Phil, Phil for Max and so on until we get to the end and Amy buys for Sue.
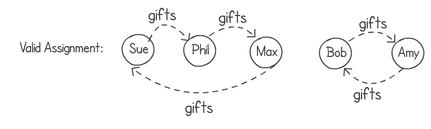
A friend of mine, after reading this "not a blog", pointed out that this did not produce all of the possible random combinations. While the idea of shuffling the list of names and then chaining them together in a ring works, it would always produce a random one-cycle ring. I have to point out that my friend, Jean Paul (https://degabriele.info/), researcher in cryptography, knows a thing or two about randomisation. He’s right of course. The following example would not be possible in my solution.
Turns out that my Secret Santa problem is actually a re-encoding of the random derangement problem in computer science. It’s quite an interesting one. The idea is to shuffle a list of elements in a way that no single item remains in the same position after the shuffling. Think about an array containing a bunch of names. After we shuffle them around, no name should be in the same place. We can then map the starting positions of each name to the finishing ones, showing who's buying a gift for whom. The next diagram shows a derangement that results in creating the two cycles shown in the previous example.
To be more precise a derangement is a permutation of elements in a set, in a way that no element appears in its original position. There is a ton of maths theory around this. For example if we just do a normal random shuffle on a list of items, the probability of having a derangement is 1/e or approximately 0.3679. The proof and theory can be found here:
https://en.wikipedia.org/wiki/Derangement
We can easily implement an algorithm that keeps on shuffling until we have a derangement. Let’s do it three steps. First let’s write something that generates a list of sequential shuffled numbers up to n-1 . For example for n = 5, we can generate 4, 1, 3, 0, 2. We can later use this sequence to swap elements in the list we want to shuffle. For example if we have the list with ["Bob", "Phil", "Sue", "Amy", "Max"] , shuffling with the sequence 4, 1, 3, 0, 2 would result with a final list of ["Max", "Phil", "Amy", "Bob", "Sue"]. Here’s the python code to generate this shuffled index. This is simply Knuth’s shuffle algorithm on a list of sequential numbers. Notice how python is one of the few languages where you can swap two elements in an array in a single line! Ah, the little joys in life...
Code Editor
The next step is to check if the generated list is a derangement or not. To do this we can simply iterate over every single item in the sequence and check if the value is the same as its index. If it is for any of the elements, then the list is not a derangement. We can easily do this with a simple ‘for loop’.
Click here to edit.
Finally we can put the two together. We can keep on generating shuffled sequences while it’s not a derangement and then swap the items in our original list using the derangement.
Click here to edit.
There are of course many better ways to implement this derangement algorithm. I'm putting a simple implementation here so it can be easily understood. This presentation outlines many other performance improvements:
https://www.cs.upc.edu/~conrado/research/talks/analco08.pdf
In our algorithm we “guess” a derangement sequence and if it’s not a valid one, we throw it away. After implementing the above code, it got me wondering, is there an algorithm that doesn’t keep on trying until it finds a valid derangement? I.e. can we have one with a measurable worst time complexity?
If we have a way to enumerate derangements, we can then generate a random number n and simply choose the n’th derangement. But how do we enumerate derangements? Maybe a good place to start is to try generating permutations. Let’s say we a have a sequence such as 0,1,2,3 … n, how do we write some code that generates all permutations of this sequence? There is a simple way to do this. It’s called the “heap algorithm”. You can find all the details about it here, implementation follows in python: http://ruslanledesma.com/2016/06/17/why-does-heap-work.html
Click here to edit.
Next we can simply ignore anything that is not a derangement. We can re-use our is_derangement() function for this. If we modify the previous program by calling this function we’ll end up with something that lists all possible derangements.
Click here to edit.
Now we just need to return the n'th derangement. This is kind of where it gets complicated with the implementation. We need to modify our function to accumulate the number of derangements generated and the n’th derangement itself. In my implementation changing the function so it returns a tuple. I’m pretty sure there is a cleaner way to do this.
Click here to edit.
Before we modify our main function to choose a random nth derangement, we need to know the upper limit of the number of derangements of the sequence. That is, given n, find the total number of derangements of a set of n elements. Wikipedia tells us that this is the following recursive expression:
countDerangments(n) = (n - 1) * (countDerangments(n - 1) + countDerangments(n - 2)) So we can implement the following function to give us the upper limit (go dynamic programming!):
Click here to edit.
Finally we can put everything together. First we select a random number between 0 and the total number of derangements. Then we use the previously developed function to get the nth number of derangements.
Click here to edit.
Right you’re probably thinking… “This is horrible” and you’re right. In fact I think this is my first time ever writing an algorithm with a O(n!) run-time complexity. The algorithm is pretty useless even for small values of n. Trying it with anything bigger than n=10 will have you waiting for a couple of lifetimes. But hey, sometimes we do things just because we can, not because it’s a good idea.
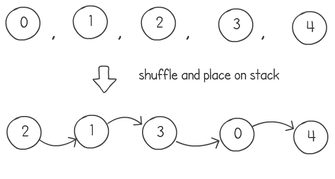
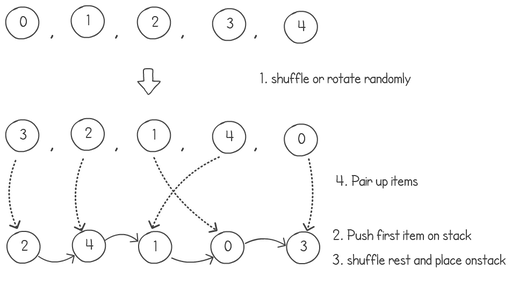
A colleague of mine, Bruno, <link to git profile> came up with a brilliant idea to find a random derangement without throwing away guesses, with a fast run-time complexity. I’m going to try to explain it in a few steps using a sequence of numbers of length 4. As usual we start with a sequence 0,1,2 ... n. The first step is to copy this list, use a normal Knuth shuffle and put the results on a stack:
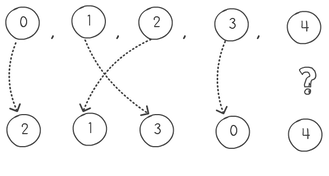
Next is to pair the initial sequence with the item of the stack. Pop one item from the stack, pair it and move to the next. If the items are equal, you pop another one pair it, and push the previous one back on the stack. In our example this produces the following pairing, meaning that 0 will go to position index 2, 1 goes to 3, 2 to 1 and 3 to zero. But we have a problem when we come to process the number 4. Basically after we pop 4, our stack is empty and we cannot pop another item.
So what do we do? Easy; we always put the first item in our sequence as the bottom item in the stack. This way the last item will never pair with the same value.
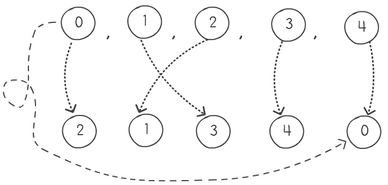
But I know what you're thinking... "The last item will always pair with the first item, it's not exactly random!". And you're right. The way to fix this is to do another shuffle on the first sequence or array-rotate it a random number of times. This way the first item on the list will always be randomly selected to match with a random selection at the end. Here are the 3 steps together.
The above example would have number 3 move to index position 2, 2 would go to 4 and so on. This gives us the derangement of [1,4,3,0,2]. Here is the complete python code of Bruno's random derangement algorithm:
Click here to edit.
Pretty neat eh? Follow my colleague Bruno on git: https://github.com/brunosousarb And check out Jean Paul's research website, there a loads of great papers on it: https://degabriele.info/
My last non-blog post got me thinking about my past technical interviews. I’ve been on the receiving end of a few of these. I remember questions like "How can you build a system where only your cat passes through the door flap?" or "Can you describe your character in 5 words?". For the record, I hated both of these… I really have no idea what they were trying to evaluate.
What about examples of good ones, the ones I really enjoyed working on? I also had a few of those. In this post I’m going to describe a past employer that asked me to write some pseudocode to implement a queue data structure. However, there was a twist… The queue had a fixed maximum size and I had to use an array as a base data structure.
Let’s start with the basics. A queue is a basic data structure used in many algorithms. It allows you to add an item to the tail of the queue (an operation called enqueue) and remove from the head (called dequeue). The way we usually model a queue is by using a doubly linked list, this gives us a constant runtime complexity for both operations. Here’s a nice diagram to explain this:
Using a doubly linked list, when we need to enqueue, we create a new node and point it to the current tail. Then we get the tail node to point to the newly created node and finally we update the tail pointer to point to the new node. To dequeue an item we do the reverse at the head of the list.
The advantage of using a linked list is that the structure grows dynamically. As long as there is enough memory you can keep on enqueuing items. So why on earth would you use a static structure such as an array to store your queued items? The idea of using an array has advantages. Notice how in the doubly linked list we’re wasting memory. For each item we have to create a container and two memory pointers. For example, if our queued items are 32 bit integers, we would be wasting 4 times the data in just pointers (assuming 64 bit pointers). In addition this constant allocating and freeing of memory space slows things down a little. So how can we model a queue so we don’t have to use all this extra memory pointers? The answer is to use a fixed sized array. The idea is to allocate enough memory for the array at initialization and then use it to store items in a queue like manner. So how would the enqueue and dequeue operations work on an array? How about you ahead and try to write the code for this and then come back to see if you got it right?
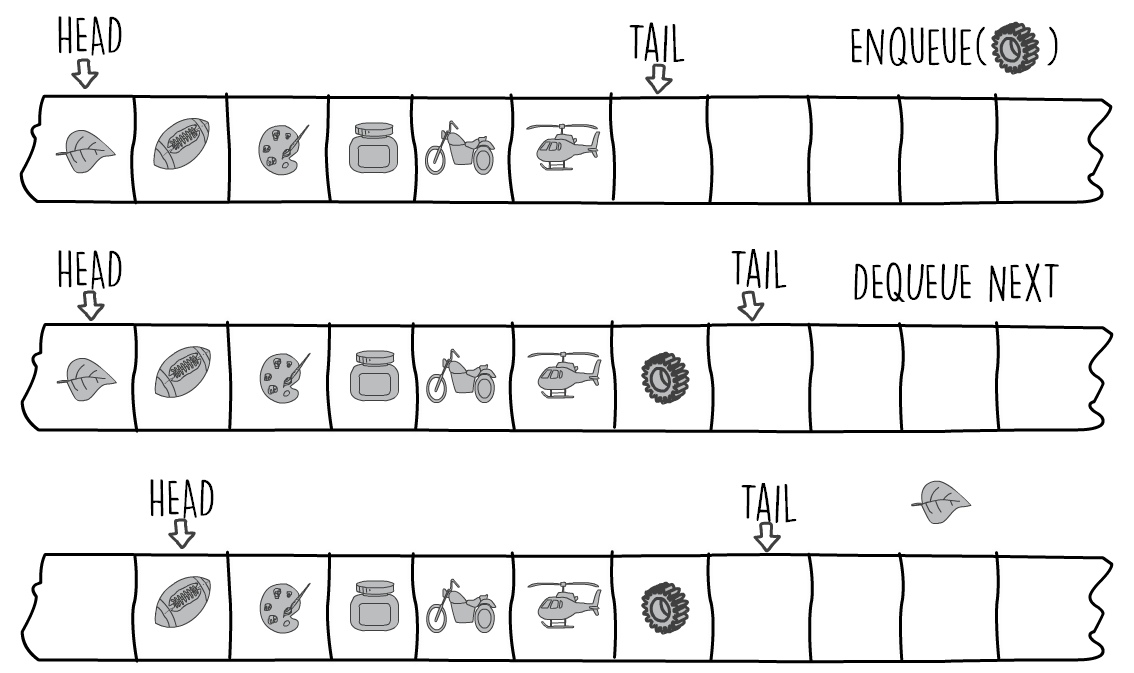
Nice to have you back. Did you manage to do it? Which parts were the hardest? I think the hardest part of the problem is caused by the fact that a queue grows from the tail and shrinks from the head. We can keep two array index pointers, one for the head and one for the tail. When we enqueue an item, we increase the tail pointer. When we dequeue, we increase the head pointer. The next diagram shows this.
This is simple eh? We always enqueue at the tail position and then increase it. The slight hiccup with our plan is what we do when the pointers reach the end of our array. The next diagram shows this. The tail pointer is at the end of our array with no more space where to advance. However the front of our array is empty and can be used to contain more items. The solution here is to wrap around (the pacman way) and move any pointer that is at the end of the queue to the front. This applies to both the tail and head pointers. How do we go about implementing this? We can easily implement the "pacman" wrap around using the mod operator. This is also the way we would implement a circular buffer. The next snippet, in python, shows how we can do this for both the tail (enqueue) and the head (dequeue) pointers. More advanced implementations can also throw errors if the array is full or empty. An array is full or empty when an increment in a pointer results in it having the same position as the other pointer. For example if we increment tail pointer resulting in the same position value as the head one we know that the queue is full. If the head pointer reaches tail pointer then the queue is empty. Both of these checks are not included in the next code to keep things simple.
Did you like this article? You can find more of these data structures and algorithms in my various courses and publications on my publications page. Please leave comments and feedback!
Meanwhile, on a Tuesday at 3:00pm: Paul: Hey James, we have an interview scheduled but John is sick and we have nobody to do it as everyone’s busy with this production issue. Would you mind going to interview this candidate for our team? Me: Hmm… I’m a bit busy but yeah sure. When is the interview? Paul: Err… yeah about that… she’s here already, waiting in room 2.08 I hurried towards the interview room with the CV in my hand, speed-reading it while trying not to trip on the stairs. When I got there, we both introduced ourselves and spoke for a while about the bad weather recently. I proceeded to talk a bit about what we do in the company, apart from sitting on bean bags (yeah I know, millennials right?) and then asked her if she could talk a little about her experience since I hadn’t managed to read her CV. I then tried to think of a coding puzzle I could ask her. See, we’ve been having some problems with coding interviews. We all have a couple of coding problems and interview problems we like to ask. The problem is that recruiters have picked up on this and we think they are preparing candidates and giving them the solutions. So we’ve all been thinking very hard about new problems. Christmas is close and our dev team decided to do a secret santa gift exchange. This is where you write everyone’s name on pieces of papers, place them in a bag and everyone draws out one name. Then you’re supposed to buy a small gift for that person. I really have no idea what I’m buying… Was considering the xkcd book, but not sure if it will arrive on time... So I thought, hmm… what if we could write a function that given a list of names would output a random pairing? I discussed the idea with the candidate and together we came up with the problem definition and a function signature. Problem: Write a function (in whatever language you want) that accepts an array of at least size 2 containing unique strings. The functions needs to output a random mapping (giver to taker) using the elements in the input such that:
Go ahead and challenge yourself to try to solve it! Then come back and read the solution. Solution: The problem can be broken down into two main areas. There is a randomization part and a pairing part (deciding who’s paired with who, so they only buy and receive a gift once). Let’s start from the easy part which is the pairing. We are 7 people in our team. One way we can decide Santa’s pairing is to walk into a room with a round table and seven chairs and make everyone sit down. Then we can have a rule that says you need to buy a gift for the person on your right. That way everyone buys and receives one gift. Except Robert that is… he has decided to not to take part. He’s now known as stingy Rob. Yes Rob, if you’re reading this, now you know. Anyway, you get the idea. In tech speak we would just need an array of names and pair each entry to the next one. Then the last element in the array is paired to the first one. This can be done functionally in Scala quite easily by zipping a list with its tail plus head: The other part is to randomize the names in the array before the pairing. This is equivalent to assigning random seats to our team on the round table. If only there was an easy algorithm that shuffles the contents of an array for us... Oh - hang on a second what about the Fisher-Yates shuffle? https://en.wikipedia.org/wiki/Fisher%E2%80%93Yates_shuffle This algorithm, also known as the Knuth shuffle, works by putting all the array entries in a “bag”. Then for each element position in the array it removes a random item from the bag and places it in that array position. It does this “bag selection” by randomly picking a position to swap to within the array. Here’s the algorithm in pseudocode: Thankfully in Scala there is already an implementation for this so we don’t need to implement it. Here is the full implementation. I’m always impressed by how expressive functional programming is. In a couple of lines of code we have implemented the entire thing! Oh yeah you’re probably wondering about the interview. She was very good and solved the problem much faster than I would have! Unfortunately, she won’t be joining my team but a different one. I’m stuck with stingy Rob.
I wanted to learn some Ruby because of an upcoming talk I am giving. I found Ruby quite easy to grasp. Ruby has some great characteristics and I enjoyed working with it. The most difficult part of coding in Ruby is stopping yourself from humming the song by the Kaiser Chiefs’ who coincidentally I’m going to see in a couple of days time. Yes, I know you’ve started humming it too now, I’m sorry… Anyway, this entry is not about the Kaiser Chiefs nor is it about Ruby. It’s about how we learn a new language or technology. If you work in development, you know how cut throat our industry can be if you don’t keep up with new technologies. Sometimes it feels like we’re in a perpetual “learn technology - use technology - learn technology” cycle. To a certain extent most other professions also require you to keep up to date. A doctor for example, needs to keep up-to-date with the latest progress in medicine and treatment methods. However, I doubt that the pace of change is quite as quick as in technology. As software developers we are constantly under pressure to learn new things as quickly as possible. So how do we go about it? Different methods work better depending on what type of person you are. You can buy books and go through them page by page working through the examples. Or you might prefer to follow a classroom or online course. I find that using aids such as books and online courses are more useful when the technology is conceptually different from what I’ve used in the past. For example if I’ve never written any functional code, I might need to follow a course if I wanted to learn Scala. Similarly if I’ve never used a relational database I will need additional help to learn how to use MySql. For everything else, I personally like learning by doing. Unlike doctors, if we want to learn something new, we can practise as much as we want without fear of causing any harm. The idea is to pick a problem and try to solve it with the new technology you’re trying to learn. Along the way you’ll learn the new features and tools available in the new language or technology. The main difficulty with this method of learning is choosing the problem or project. If you attempt to pick a random project such as “Let’s develop an online flower shop” it will not work. You’ll quickly get bored of it. When you start hitting difficult problems you start to question why you picked such a useless project in the first place and putting so much effort into it. Soon you’ll drop it and say “eh, I’ll stick with visual basic for the rest of my life”. Pick something that is useful and real. If you are learning javascript as you plan to open an online business, make that online business your learning project. If you need to learn python to start writing deployment scripts at work, learn python while doing that. Of course you’ll need to fail many times before you succeed, so try your pet code in an isolated environment before moving to the real thing. Back to me learning Ruby now. I’m giving a workshop to a coding bootcamp, called “Le Wagon”, https://www.lewagon.com/lisbon in Lisbon in a couple of weeks. The talk’s title is “Beating the coding interview” and is about learning a few tips to solve the puzzles one gets given during an interview. At Le Wagon, students use Ruby as their web development language. I must confess that up until a few weeks ago I knew almost nothing about Ruby. Keeping in mind that I also have a full-time job, how could I learn the essentials in Ruby in the shortest amount of time? Since the talk is about coding interview puzzles, what better way to learn it than to try to solve some of these puzzles in Ruby? The internet is full of example puzzles. One of the most popular sites offering these coding exercises to candidates is http://www.codility.com/. They have a practise area where you can try solving sample coding puzzles in many different languages, amongst them Ruby. My plan of action was to pick a few these sample questions and solve them, learning about the different bits of language along the way. Here’s how it works in practise. The brackets problem from codility is about writing a function that checks if a string has a properly nested set of brackets "[]{}()". Here are some examples to get the idea: text = "[()()]", result = true text = "[(]()]", result = false text = "[{()}]", result = true text = "[(])", result = false The solution is quite straightforward if you have worked with stacks before. The idea is to process the string, one character at a time, left to right. If you encounter a left bracket you push it on the stack. If you encounter a right bracket you pop the first item on the stack and check that the brackets match (round with round, curly with curly etc…). In the end you make sure you have emptied the stack. Therefore, for the solution, I needed to find out how to use a stack in Ruby and how to do conditional branching (ideally using some sort of case statement). I also needed to loop over every character in the string and check if the stack is empty at the end. Right, a few google searches later I found out: 1. Iterating over every character in a string: Code Editor
2. Using a case statement: 3. Using a stack: 4. Checking if an array is empty: 5. Using an if statement: Now that I had the building blocks all that was left was to put everything together and to try it out (The app on Codility confirmed the next solution is correct): My solutions to codility lessons problems can be found at https://github.com/cutajarj/CodilityInRuby
Happy learning by doing! Using the correct algorithm can make a difference between a happy afternoon coding and a mental breakdown. This applies to other aspects of life… The baker needs to apply the right mix and technique for the bread; unless you want to make your life miserable you need the correct sequence of steps to change the motorbike oil; the list goes on and on. This analogy is especially true for programming problems. I will illustrate this concept by means of a simple example problem: Write a function “evaluate” that accepts an infix expression “expr” as a string and returns the expression evaluated as a double. Function signature:
Examples:
Limitations:
Right… So there are now two kinds of people reading this post. The first kind most likely met this problem before maybe during their university course and know the general idea of the algorithm. The second type is thinking “How hard can this be?!”. I dare the second kind of readers to try it out without googling for a solution or using libraries. Come on, stop reading this post and come back once you’re finished. I know you want to. You’re back? How did it go? How many grey hairs have you grown? Is Trump still President? If you belong to the first kind and you’ve seen the solution before, you’ll be able to solve it in about an hour or two maybe after brushing up on some specifics on the algorithm. For the rest, I will now show you the solution using Scala, because Scala is awesome. First some definitions. Infix refers to the way we normally write expressions. I.e. when the operator is the middle between two operands. Infix: operand1 operator operand2 Examples:
Postfix is another way to represent an expression. In postfix the operator is after the operands. Postfix expressions don’t support (or need) parentheses.Postfix: operand1 operand2 operator Examples:
Although it doesn’t feel like it, it’s way easier to evaluate a postfix expression. When evaluating infix expressions, you need to take care to evaluate it in the right sequence, doing the parenthesis first, then division and so on. Using postfix the natural sequence of the expression dictates the precedence. A postfix is evaluated by traversing the expression left to right and whenever you meet an operator you replace the operator and the two previous operands with the result. For example consider the expression 1 + 2 * 3 + 4 which translates and evaluates to:
Writing the above in Scala in a more functional way leads to something like: Notice how easy it is to implement this using foldLeft and Scala’s pattern matching. The foldLeft is initialized with an empty list representing the stack. Matching is then done on the two top stack elements and operator type. The result is found and pushed on top of the stack. At the end we simply read the top of the stack to get the final result. Ok, so now we have a way to evaluate a postfix expression. All we need now is a way to convert infix to postfix and we are done. The algorithm is also quite simple:
Again, notice the versatility of pattern matching in Scala. In the above algorithm we start the foldleft with an empty postFix list and an empty stack. We then match on the input infix operands and operators and perform the required logic in each case. The “span” function was used here to split the stack in two. This can be described as popping the stack until the given condition is no longer met. For example: Would keep on removing items from the top of the stack until the left parenthesis is found: ( List(*, +), List((, -, +) ) All that is left now is to call the two functions in sequence: There… Job done. This problem is a good example that transforming the input into a different encoding and solving turns out to be more simple than trying to evaluate the expression using the original infix notation. For reference the above algorithm is a simplified version of the “Shunting-yard” algorithm by Edsger Dijkstra.
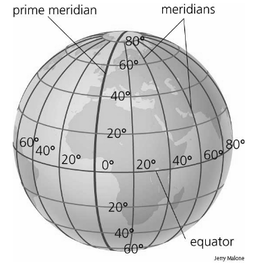
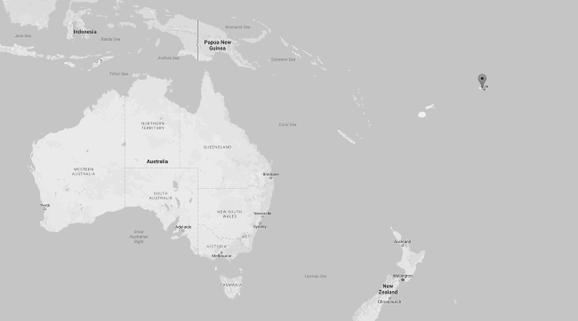
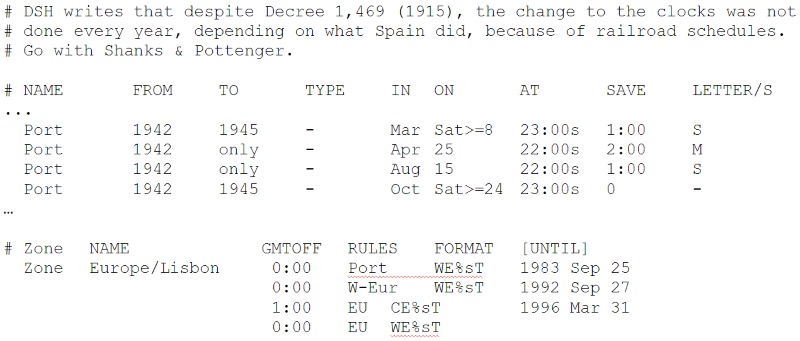
Make sure you run your motorbike for a few minutes before changing the oil. This warms up the oil and helps it flow when draining. It's been a while since I’ve written one of these. Last time I wrote an entry in here I only had one child, worked at another office and lived in a different country. I've been busy and life got in the way... So it's fitting my next post is about timekeeping! How many times, as a developer, have you had to deal with a timezone or daylight savings bug? Myself, I have had to deal with so many that I don't think I can list them all. Probably the most entertaining one was when I was working at a factory site where IT had just installed a new payroll system. The factory worked night shifts and workers were paid by the hour. An employee would tag in and out using a palm reader. Pay would then be calculated based on the number of hours spent on their shift based on the time between when he tagged in and out. You’d think it's easy stuff right? Think again... The system was happily running for almost a year before a number of workers made a fuss about being paid 1 hour less on one of the night shifts. It turned out that on the night when daylight savings ended, the computer turned the clock back one hour. This meant that anyone working that night shift had worked one hour more than what the application had calculated. The HR department noted however that nobody had complained six months previously, when the daylight savings came into effect and everyone got paid for one extra hour that wasn’t real. Bugs in timezones/daylight savings can be more serious. A bank I worked with few years ago moved hosting servers from one country to another. The new servers were mistakenly configured to run under a different timezone. This caused a bunch of stock options to be exercised a few hours late. The bank made big losses of money and reputation. Is keeping time so complicated? It turns out it is... pretty much. Let's try to look at why this is. So what’s a timezone?The idea behind timezones is that wherever you are in the world the sun should rise and set at more or less the same time. Have a look at the picture above. This shows a simplified view of how this should work. The world is first divided into vertical slices (called meridians). An arbitrary one is then picked and called the prime meridian. Going west you reduce the hours with reference to the prime meridian, going east you increase it. You keep on doing this until you meet on the other side of the world. Once there, you take a swim in the Pacific, toss a coin on whether it should be a -12 or a +12 and congratulate yourself on a job well done. One of the problems is that timezones weren't decided by one guy on gap year going around the world. They were decided and modified throughout history by various governments in many countries. To say this caused a lot of complications is the understatement of the year. Why, you might ask? Let me demonstrate with an example. Can you guess what's so special about the group of islands of Samoa shown here in the picture? The government of Samoa didn't like that it was the last country on earth to go to sleep. In December 2011 they decided Samoa would switch timezone from UTC-11 to UTC+13! Yes you read correctly. Timezone UTC+13 should not even exist. The government did cite economic reasons for doing this, such as their biggest trade partner being Australia, but really we all know they did it so they can be the first to say “Happy New Year!”. This created all sorts of weirdness. For example anyone living in Samoa had to wipe out an entire day off their calendar, the 30 December 2011. I wonder what people did if they had a flight booked on that day or say a dentist appointment? American Samoa, just 30km east is now 25hrs behind. Crazy stuff eh? The history book is full of examples like these. Nepal has a timezone of +5:45, Mumbai +5:30 and countries like Portugal and Spain have different timezones even though they overlap! It's fair to say that keeping time across countries is a hairy business. The situation gets even more complex when you introduce daylight savings. Daylight savings was introduced during the war (apparently to save fuel). The idea is that in summer when days are longer time is moved forward by one hour. Although apparently there is a place called Lord Howe Island (Australia) that only moves half an hour... What is the problem doc?Let me explain by using an example. Let's say you arranged a meeting at 1:30am on the 25th October (in the UK). Most countries in Europe, on this date, move the hour back to winter time. At 2am the clock is moved back to 1am and everyone gets to sleep an hour more, well unless you have a meeting at 1:30am. Now if you think about it, you will live through 1:30am twice on that night. Will the meeting happen on the first 1:30am, the second or will you just have to hold it twice? This isn't a big problem right? Nobody holds meetings at this hour. Well what if you had a flight departing at that time? Or maybe you have a night shift starting at that hour? Or a nuclear reactor where the rods need to be retracted at exactly 1:30am ONCE? There are loads of other problems such as: 1. Countries change timezones 2. Countries change daylight savings rules 3. Converting between timezone for a specific historical date requires political history 4. Switching from winter to summer time and back causes problems Ok fine, let's look at the tools available so we can make time keeping easier. Standard TimesThese come in various names, GMT, UTC, Zulu time and many others. They have basically the same idea. Have a time defined that isn’t affected by timezone or daylight. Standard times evolved from when British naval captains used to keep one of their watches to the time at home (UK is on the zero meridian). The timezones of the different countries they sailed to used to be defined relative to this time. This standard time is what is known today as GMT (Greenwich mean time). From this evolved UTC (coordinated universal time) which is what is used today. A timezone is usually referred to as UTC+/-X. Why is standard time useful for us? Because it gives us an easy way to convert from one timezone to another. If the time is 2pm in NY UTC-5 what is the time in Spain UTC+1? Simply add 5 to convert to UTC and add another 1 to convert UTC to Spain. Timezone databaseIANA maintains a historical timezone record for all countries. This lists all the timezones and daylight savings applied to countries over the years. Typically the database goes back up to the 19th century. It also contains future changes to timezones that have been publicly announced by the governments. The database is updated frequently. Here’s an excerpt taken from an update done in March 2015: “Mongolia will start observing DST again this year, from the last Saturday in March at 02:00 to the last Saturday in September at 00:00. (Thanks to Ganbold Tsagaankhuu.) Palestine will start DST on March 28, not March 27. Also, correct the fall 2014 transition from September 26 to October 24. Adjust future predictions accordingly. (Thanks to Steffen Thorsen.)” The database keeps its histories in two sections; one dealing with timezones and the other with daylight savings. Here’s another excerpt taken from the actual database: The history shows that in 1942 Portugal moved the clock forward twice, in March and then in April. In August and then in October it moved the clock backwards again. Apparently this double DST happened in the UK too during WW2. Fascinating, right? In the second section we see that Portugal was on the same timezone as Spain (GMT+1). This lasted from 1992 to 1996. My guess is that after 4 year of eating dinner late they decided that having dinner in the middle of the night like the Spaniards was just too late for them. LibrariesLibraries and tools for the IANA database exist in every programming language. Many languages (such as a JVM language) come bundled with timezone libraries, however these need to be updated from time to time to the latest IANA database. For example in Java you can update to the latest database either by keeping up to date with the last JVM release or simply running a tzupdater tool periodically (just google “tzupdater Java tool” for more details). Ok now what?So we saw the tools available to tackle the complexities of timekeeping. How do we use it? The answer is surprisingly simple. To explain this let’s look at an industry which has solved this problem already. The aviation industry has solved this problem by completely ignoring it. Instead of dealing with each individual country and its timekeeping politics, they decided “screw it, we’re keeping our own time and we shall call it the ZULU time”. The Zulu time happens to be equivalent to UTC, the difference is that it’s written in a different format. For example here’s a weather report used by pilots (pilots use this format as it’s concise, unambiguous and they can read it really quickly): EIDW 241430Z 11007KT 050V150 9999 FEW024 SCT250 20/12 Q1021 NOSIG The bit in bold (1430Z) shows the time this report was issued, 2:30pm UTC. Aviation uses this time format for everything and anywhere on earth. Examples include radio communications, airport time slots, ETAs, forecasts, log reporting etc… This simplifies things and makes everything unambiguous, thus avoiding situations like “Controller: Err… when you say, you’ll be over Italy at 12:35 is that in the departure, arrival or Italian timezone?” The idea here is to use the same technique when writing our applications. Every time you start thinking about a clever algorithm to convert timezones or to negate the effects of DST: It’s a pretty simple solution right?
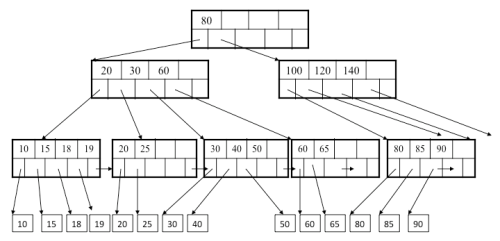
Any exceptions? Well obviously yes. But it’s only a simple one really. Only convert to the local timezone when you want to display a date to a user. For this you just display the UTC date converted to the timezone that the user is located in. EASY! Come to think of it this is what aviation does too: “Ladies and gentlemen, welcome to Malta Airport where the local time is 9:30am and the temperature is 32 degrees. For your safety and comfort, please remain seated with your seatbelt fastened until the Captain turns off the Fasten Seat Belt sign.” Ok here's the exercise: find me a data structure which can accept random key/value inserts and which I can query faster than O(log2(n)). I might be wrong on this one but I don't think one exists. I know what you're thinking... Hashtables. Well think again, remember CS101? Hashtables have a big O of n. Hashtables, while they're on average really fast have a worst case of N. There is an easy way to remember this in case you're asked in an interview. Think of a chained hashtable with a very bad hash function where every key is added to the same entry. This will result in all the keys in the same chain giving a search performance of O(n). So what else have we got? Arrays are O(1), but they're not suitable for random key/value inserts. Well unless you have infinite memory. Anything involving a list (Linked, Arrays and vector lists) is slow with O(n). So the only thing remaining is tree structures. A binary tree is actually also O(n). Think of inserting a sequence of numbers 1-100 in ascending order... you'll also end up with a sort of linked list. Balanced binary tree, on the other hand, is a different animal. This guarantees searches in O(log2(n)). There are various flavours of these, such as AVL and red-black trees all of which make good reading on Wikipedia. Here: http://en.wikipedia.org/wiki/Self-balancing_binary_search_tree Still, my claim that you can't search faster than O(log2(n)) stands. So what about faster tree structures? Things such as B-trees where nodes can have more than 2 children? Ok. So let's ignore the important mathematical fact that O(logx(n)) = O(logy(n)) as practically speaking log100(n) will be a bit faster than log2(n). However, again practically speaking, a B-tree with order x does not have a performance of logx(n), it is still log2(n). Shocker! The height of a B-tree might be logx(n), but this does not reflect its search performance. To understand this, you need to consider what happens in each node. In a B-tree (or any other higher order tree structure), you need to store a list of keys and pointers to the children. Here's a picture of what B-tree nodes look like: As you see the keys can be stored in an ordered fashion at each node. This lets us do a quick binary search on each level hop. And the performance of this binary search is? Yes log2(x). If x is the order of the tree, this gives us: height of tree: logx(n) performance of each key node search: log2(x) total performance: logx(n) * log2(x) simplifying: log(n)/log(x) * log(x)/log(2) log(n)/log(2) log2(n) TADA! What happens when you keep on incrementing an integer past its maximum? Most competent developers would answer 'It would go to something negative'. Some would even be able to explain why and detail the way two's complement works. But what happens when you get a double and keep on dividing by two past its precision limit? Most would answer 'Er... I don't know. I have to try it' or 'Hey, let's play online pong'.
Floating point representation in binary can be a pita to grasp. Not because it's more complex than the simple two's complement but it's because it's something you don't really care about since it just works. . You would rather watch cat clips than spend time reading about it. The problem is that we work with floats all the time, from them representing money to asteroid speeds. I've seen so many simple coding bugs because a lot of developers don't get the basics of floating point representation. So here's a quick refresher which hopefully is more interesting than watching cats on YouTube: Floats and doubles in Java (and most other languages) use the IEEE754 standard which stores things as: C x B^E => example 2.625 x 10^2 where C = 2.625, B=10, E=2. C is called the coefficient, B is the base and E is the exponent. But who cares what they're called, right? Now the IEEE standard is pretty complex and specifies various formats but in summary 'Singles' (java floats) use 1 bit for the sign, 23 bits for the coefficient and 8 bits for the exponent. Doubles use 52 bits for the coefficient and 11 for the exponent. The standard specifies two values you can use as base, 2 and 10. Languages such as C, Java C# and many others use the base 2 representation for the float and double primitive types. So let's pick the example 2.625 again and see how to represent it. This can be expressed as 2.125 x 10^2 with: C = 2.625 B = 10 E = 2 Next step is to convert to base two. Converting the coefficient is done by using something like: ...[8][4][2][1].[0.5][0.25][0.125][0.0625]... 0 0 1 0 . 1 0 1 0 Thus: C = 10.101 B = 2 E = 10 Does this sound like thermo nuclear dynamics? Not really... So you might ask... why do so many of my website users report problems with their balance? Why is this guy’s balance showing as 2000.0000000003176?! Here's a quick test (yes it's scala) that shows the main problem of base 2 floats scala> (0 until 10).foldLeft(0.0)( (x,_) => x+0.2) res13: Double = 1.9999999999999998 What is going on here? It's simply adding 0.2 ten times. Why is it losing precision even on such a simple operation? Does this look familiar to you? Probably. I see this type of problem over and over again and it confuses a lot of programmers. Often this confusion results in 'creative' hacks. Most common thing to do is to round to some precision after each addition or using BigDecimal. BUT THIS IS THE WRONG WAY! 'I know I've hurt you, and I've not been true ... But I know I can turn it around' Ok... Keeping drum and bass artists out of this, let's understand what's happening here. The explanation is pretty simple. How would you represent 1/5 in binary? You can't... You can only estimate it. Try it using the above conversion process. You'll end up with something like: 0.010101010101... However, 1/5 can be represented in decimal accurately as 0.2. What about for example 2/3? In decimal you can only estimate it (0.666667). Basically the base you decide to use dictates what rational numbers you can represent accurately or not. 1/3 can be accurately represented if you're using base 3 or 12 but not in base 2 or 10. We would probably be a more advanced race if we had 12 fingers... (see http://en.wikipedia.org/wiki/Duodecimal#Advocacy_and_.22dozenalism.22) So what do you do about it? NOTHING! So what if humans speak base 10 and computers base 2? We shouldn't force machines to use base 10 (such as using BigDecimal) or hack around and 'round' floats everywhere. We simply need to convert estimated base 2 floats to proper base 10 when presented to users. For example if a user's balance is $150.20 it's fine to store this in memory/DB as 150.1999999999999999 using the full float/double precision without any rounding. But when you're displaying the balance to the user you just show it by rounding it to $150.20. The rule here is to never round and store. The only rounding happens for presentation and it's never stored. Wouldn't my application start leaking cents/pennies? Yes... but you shouldn't lose sleep over it. Let’s look at an example. Say you're using double to sum up every transaction that happens in your shop. Say you sell 500 things a second, 24x7 and every single operation is a double which can't be represented precisely in base 2 (very unlikely). In this scenario you'll end up losing something like 2c a year. While this inaccuracy might be crucial if say you're sending monkeys to the moon, it's unlikely to bankrupt your online business selling cat grooming products. The firm I'm working with was in the process of hiring some new developers. I was asked to come up with some programming tasks they could ask candidates during the interviews. These were of the problem-solving type, ones where you need to write an algorithm and solve a particular problem. The interviewer sits with you during this process and assesses your problem-solving and communication skills. I've been on both sides of these kinds of interviews many times. In general I think they are a good idea. Problem-solving and good communication are the best skills a developer can have. These tests can give you an insight into both. But here's the catch. The problem needs to be right and the interview conducted in the correct manner. Asking the developer to implement a distributed b-tree in 30 minutes is not really going to prove anything except that you're a big nerd. So we researched hard about what problems to give candidates. We came up with a handful of programming tasks, roughly of equal difficulty that could realistically be completed in 45 minutes. Each interviewee was then given a random problem to solve and was encouraged to ask questions and speak their thoughts (explain their reasoning?) as they were 'searching' for the solution. When talking about this to another developer friend he told me how he had recently had a similar programming interview (with another firm) and failed. I asked him to describe the question he was asked and he told me it was done online with a website called 'codility' and that he had only 30 minutes to complete. He emailed me a summary of the problem and it was something along these lines: Problem 'Count the cycle' You are given an array of integers: int numbers[] Each element in this array represents an index on the same array. Your algorithm needs to follow the path from index 0 and count how many elements are 'stuck' in a cycle. Your function should return this count. This is best explained in an example (array indexes start from 0): numbers = {3,2,4,4,1} Starting from index 0 you read its value(3) and jump to index 3. You then read this value(4) and jump to index 4 and so on. So following this process you'll end up getting: '3,4,1,2,4,1,2,4,1,2,4...' In the above the cycle it would be 1,2,4 and it should return 3. Easy right? No... an extra constraint is that it needs to have a worst time complexity of O(n) and worst space complexity of O(1). The question also specifies that the input array does not count as 'space'. So basically you can modify it without incurring any space complexity hit. Here's my trail of thought on this, the first time I read the problem: Reading question... Reading question... Oh this is way too easy. This is just a linked list in an array, just put stuff in another linked list and count backwards after the first... 3 minutes Crap there is a space limit of O(1)! No way this can work! How can it be possible? Oh hold on... I can modify the array.. aha... Ok think... think... 5 minutes I have to store some 'cycle' state in the array itself. Hmmm... crap 10minutes have passed already... ok focus. We need at least two sorts of flags. One when we are doing the first pass and another when we're stuck in the cycle counting nodes. 12 minutes Ok ok... I think I got it. How about negating numbers on the first pass and stopping when you hit the first negative number? Then a second pass making numbers positive, this time counting until you hit the positive tail. Something like: int index = 0; 18 minutes NO! This won't work if we have a zero! Balls... Ok maybe we can shift everything forward by adding 1... actually hold on we can shift everything forward on the first pass and then everything backwards on the second. Right yes this should work. I just need to add a large number to everything and then subtract it on the second pass. The large number can simply be the array length: int index = 0; 25 minutes Does this work? Let me write some tests... yep looks like it's fine. Is it time O(n)? Well it's really O(2n) but that’s fine as O(n)==O(2n) yep. Is it space O(1)? Yep same argument as for time. 30 minutes Phew... Just made it in time... I wonder if I would have made it under pressure in a real interview? Probably not. I didn't feel great with my solution having solved it with only seconds to spare. So I decided to pass it on to some other developers at work and see how they got on. So one guy solved it in about the same time as me (on a piece of paper) and two others spent almost a full day thinking about it and finally quit and came to ask me for the solution. Does it mean anything? Am I better than my colleagues who couldn't solve it? While it does make me feel better about myself, the reality is that I was lucky to have a light bulb moment while the others didn’t. This doesn't mean that my way of thinking is better. I discussed this with one of the guys that couldn't get it and he told me that he was thinking of ways to solve it with the space constraint but he couldn’t figure out how to encode the 'cycle' information in the array itself. In fact, as soon as I gave him a small hint on shifting numbers he quickly got to a similar solution (he shifted the numbers twice forward instead of one forward and one back). This is why I believe the choice of question is very important. Choosing the wrong question is like asking someone to solve the famous 'Crossing the river with a wolf, a goat and a cabbage' problem. Anyone who comes up with a right answer in a few minutes does so because: 1. He has seen/heard it before 2. He's lucky and had a eureka moment thinking 'hey the goat can cross back' 3. He's a farmer and has goats, wolves and cabbages crossing rivers all the time The moral here is that the 'wolf/goat/cabbage' problem just like the 'Count the cycle' problem does not prove you're any better for the job or that you are more intelligent or that your problem-solving skills are any better. In fact, it doesn't show much at all. So what should the interview programming questions look like then? In my view it's difficult to get it just right. The problem needs to be easy enough to dot in the time allocated but hard enough so not everyone can do it. It should avoid being a puzzle but instead be a problem where the candidate can show his/her problem-solving skills and algorithm design. Problems that can be broken down into multiple smaller ones tend to be better and so are ones which require the use of multiple datastructures types. Problems like: 1. You have an array of random integers. Find the first non-duplicate number in the array in O(NlogN). 2. You have two sorted arrays of size N and M where N <= M. Output the intersection in O(N) 3. How can you implement a linked list in an array (fixed size limit). I know. The above are not exactly rocket science but neither is the 'Count the cycle' problem once you solve the encoding puzzle. And as for the wolf/goat/cabbage problem the cabbage didn't ask to cross bridges anyway.  Disclaimer: this is in no way saying codility is a load of rubbish. I've worked on some of their sample problems and I think they're very good for filtering out candidates that have no idea about computer science. It still amazes me that sometimes we get someone with years of experience on his CV who cannot write a simple findMax(array) function. So codility is a great tool for filtering some of the worst. I just think that whoever uses codility or similar services needs to be careful about the problems they choose and try to stay away from bad ones like the above. |
AuthorJames Cutajar is a software developer, with interests in high performance computing, algorithms design and distributed data structures. Archives
April 2020
|