|
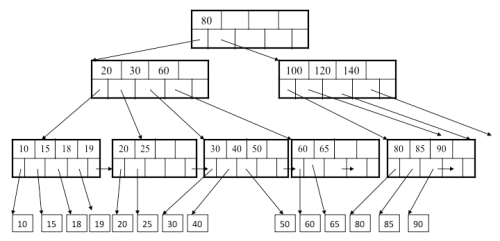
Ok here's the exercise: find me a data structure which can accept random key/value inserts and which I can query faster than O(log2(n)). I might be wrong on this one but I don't think one exists. I know what you're thinking... Hashtables. Well think again, remember CS101? Hashtables have a big O of n. Hashtables, while they're on average really fast have a worst case of N. There is an easy way to remember this in case you're asked in an interview. Think of a chained hashtable with a very bad hash function where every key is added to the same entry. This will result in all the keys in the same chain giving a search performance of O(n). So what else have we got? Arrays are O(1), but they're not suitable for random key/value inserts. Well unless you have infinite memory. Anything involving a list (Linked, Arrays and vector lists) is slow with O(n). So the only thing remaining is tree structures. A binary tree is actually also O(n). Think of inserting a sequence of numbers 1-100 in ascending order... you'll also end up with a sort of linked list. Balanced binary tree, on the other hand, is a different animal. This guarantees searches in O(log2(n)). There are various flavours of these, such as AVL and red-black trees all of which make good reading on Wikipedia. Here: http://en.wikipedia.org/wiki/Self-balancing_binary_search_tree Still, my claim that you can't search faster than O(log2(n)) stands. So what about faster tree structures? Things such as B-trees where nodes can have more than 2 children? Ok. So let's ignore the important mathematical fact that O(logx(n)) = O(logy(n)) as practically speaking log100(n) will be a bit faster than log2(n). However, again practically speaking, a B-tree with order x does not have a performance of logx(n), it is still log2(n). Shocker! The height of a B-tree might be logx(n), but this does not reflect its search performance. To understand this, you need to consider what happens in each node. In a B-tree (or any other higher order tree structure), you need to store a list of keys and pointers to the children. Here's a picture of what B-tree nodes look like: As you see the keys can be stored in an ordered fashion at each node. This lets us do a quick binary search on each level hop. And the performance of this binary search is? Yes log2(x). If x is the order of the tree, this gives us: height of tree: logx(n) performance of each key node search: log2(x) total performance: logx(n) * log2(x) simplifying: log(n)/log(x) * log(x)/log(2) log(n)/log(2) log2(n) TADA!
0 Comments
Leave a Reply. |
AuthorJames Cutajar is a software developer, with interests in high performance computing, algorithms design and distributed data structures. Archives
April 2020
|